มหัศจรรย์ แห่ง ดอกเบี้ยทบต้น (compound interest)
พลังของดอกเบี้ยทบต้น
สถิติตั้งแต่เปิดตลาดหลักทรัพย์แห่งประเทศไทย พ.ศ. 2518 ถึง 2554 อัตราผลตอบแทนเฉลี่ยอยู่ประมาณ 12% ต่อปี
แสดงว่าถ้าเราลงทุนในหุ้น Blue Ship ผลตอบแทนจากเงินปันผล+capital gain จะอยู่ที่ 12% ต่อปี ในที่นี้จะใช้10% เพื่อคำนวณ
ตามกฎของดอกเบี้ยทบต้นบอกว่า
ถ้าเราสามารถทำผลตอบแทนได้ 10% ต่อปีและนำผลตอบแทนที่ได้ใส่กลับเข้าไปลงทุนต่อ ทุกๆ 7 ปีเงินของเราจะกลายเป็น 2 เท่า
เงินลงทุน 1,000,000 บาท
ปีที่ 1 เงินต้น 1,000,000 บาท ผลตอบแทนสิ้นปี 10% = 100,000 บาท
ปีที่ 2 เงินต้น 1,100,000 บาท ผลตอบแทนสิ้นปี 10% = 110,000 บาท
ปีที่ 3 เงินต้น 1,210,000 บาท ผลตอบแทนสิ้นปี 10% = 121,000 บาท
ปีที่ 4 เงินต้น 1,331,000 บาท ผลตอบแทนสิ้นปี 10% = 133,100 บาท
ปีที่ 5 เงินต้น 1,464,100 บาท ผลตอบแทนสิ้นปี 10% = 146,410 บาท
ปีที่ 6 เงินต้น 1,610,510 บาท ผลตอบแทนสิ้นปี 10% = 161,051 บาท
ปีที่ 7 เงินต้น 1,771,561 บาท ผลตอบแทนสิ้นปี 10% = 177,156.1 บาท
สิ้นปีที่ 7 จะมีเงินเท่ากับ 1,948,717.10 บาท ก็ประมาณเกือบ 2 เท่า
ประเด็นสำคัญอยู่ที่ เราสามารถทำได้สูงกว่า 10% ได้หรือไม่? ถ้าทำได้ ระยะเวลาของคุณก็จะสั้นลง จาก 7 ปี เป็น 5ปี 3ปี ปีเดียว
มหัศจรรย์ แห่ง ดอกเบี้ยทบต้น (compound interest)
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”― Albert Einstein
อัลเบิร์ต บอกไว้ว่า “ดอกเบี้ยทบต้น นั้น เป็นสิ่งมหัศจรรย์ของโลก ลำดับที่ 8 ใครเข้าใจมันได้ก่อน คนนั้นก็ไม่ต้องเสียโอกาสจากมัน”
Compound interest หรือ ดอกเบี้ยทบต้น หลักการของมันคือ การรวมเอาดอกเบี้ย เข้ากับ เงินต้น เพื่อนำไปคิดเป็นเงินต้นใหม่ในงวดต่อๆ ไป (เงินต้นที่มีดอกเบี้ยงวดที่แล้วรวมอยู่ด้วย) ทำให้ดอกเบี้ยในงวดต่อๆ ไป มากขึ้น เรื่อยๆ เพราะ เงินต้นที่นำมาคิดในแต่ละงวด มีมากขึ้นจากการรวมดอกเบี้ยในงวดก่อนหน้านี้เข้าไป
ความมหัศจรรย์ ของ ดอกเบี้ยทบต้น มันอยู่ที่ว่า ถ้าให้เวลากับมัน เราจะพบถึงพลังที่แท้จริงของมัน
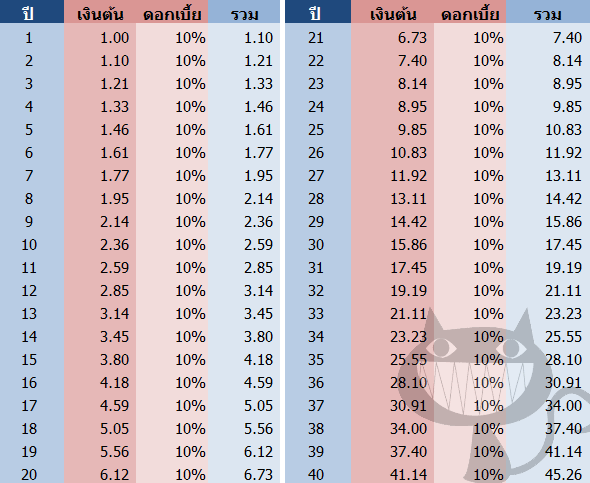
Ex. ถ้าคิดคำนวนดอกเบี้ยแบบทบต้น ทุกปี ดอกเบี้ย ปีละ 10% สม่ำเสมอ ไปเรื่อยๆ 10 ปี (10 งวด) จะมีมูลค่าเพิ่มขึ้น ถึง 2.59 เท่า (259%)
ปี ที่ 40 หรืองวดที่ 40 มูลค่าเพิ่ม ขึ้น 45.26 เท่า (4526%) ดังนั้น
“ถ้า ในปีแรก มีเงินต้น 1,000,000 บาท ดอกเบี้ยคงที่ทุกปี ปีละ 10% แล้วคุณปล่อยให้ดอกเบี้ยทบต้นไปเรื่อยๆ ในทุกๆ ปี ทุกๆ งวด ในปีที่ 40 จะพบว่ามีเงิน มูลค่า = 1,000,000 x 45.26 = 45,260,000 บาท
สูตร การคิดหาเงินในอนาคต แบบดอกเบี้ยทบต้น
Fv = Pv(1+r)^t
Fv = เงินในอนาคตที่คาดว่าจะมี (บาท)
Pv = เงินต้นในปัจจุบัน (บาท)
r = อัตราดอกเบี้ย ต่องวด (%) (ในตัวอย่าง ใช้ งวดหนึ่ง เท่ากับ 1 ปี)
t = ระยะเวลาในการคิดดอกเบี้ยแบบทบต้น (จากตัวอย่าง 40 ปี t จึง เท่ากับ 40 )
ถ้าอธิบายตามสมการแล้ว t นี้ เป็นตัวยกกำลัง ถ้าจะถามหา ว่า ปัจจัยไหน ที่มีความแรงสุดในสมการ แน่นอน ก็ต้องตอบ ว่า t เพราะมันยกกำลังอยู่นั้นเอง มัน เพิ่มที เป็นทวีคูณ ตรงกับ ที่ได้ เคยบอกไว้ ข้างบนว่า ความมหัศจรรย์ นั้น อยู่ที่ การให้ระยะเวลากับมัน
เป็นหนี้ บัตรเครดิต ยอดหนี้ บางราย หนี้ส่วนใหญ่ที่ติดค้าง เป็นดอกเบี้ย มากกว่า เงินต้นที่ใช้บัตรไป บัตรเครดิต เป็นตัวอย่างที่เห็นได้ชัดเจน เพราะบัตรเครดิต ใช้วิธีการ คิด แบบนี้ สำหรับ ผู้ที่ติดค้างการชำระ ในรายงวดนั้นๆ เค้าจะคิดดอกเบี้ย จากเงินต้นที่เหลือค้างชำระจากยอดการใช้เครดิต ในงวดนั้น เมื่อถึงงวดต่อไป เงินต้นที่เค้าจะนำมาคิด มันจะรวมดอกเบี้ย จากงวดที่ติดค้างก่อนหน้านั้นด้วย เราจึงเห็น คนที่เป็นหนี้บัตรเครดิต และไม่สามรถผ่อนชำระ ได้หมด อยู่บ่อยๆ เพราะหนี้ที่เกิดขึ้นนั้น ยิ่งนาน ยอดยิ่งเพิ่มขึ้น เรื่อยๆ จนถึงจุดที่ เพิ่มเป็นทวีคูณ ไอน์สไตน์ ถึงได้บอกแบบนั้น
“Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.”
“ถ้าใครเข้าใจมัน ก็ไม่ต้องเสียประโยชน์จากมัน” ดังนั้น เมื่อเราเข้าใจ วิธีการของมันแล้ว ถ้าเรารู้จักนำไปใช้ ในทางที่เป็นประโยชน์ กับเรา ผลที่ได้จะกลับมาหาเรา อย่างมหาศาล